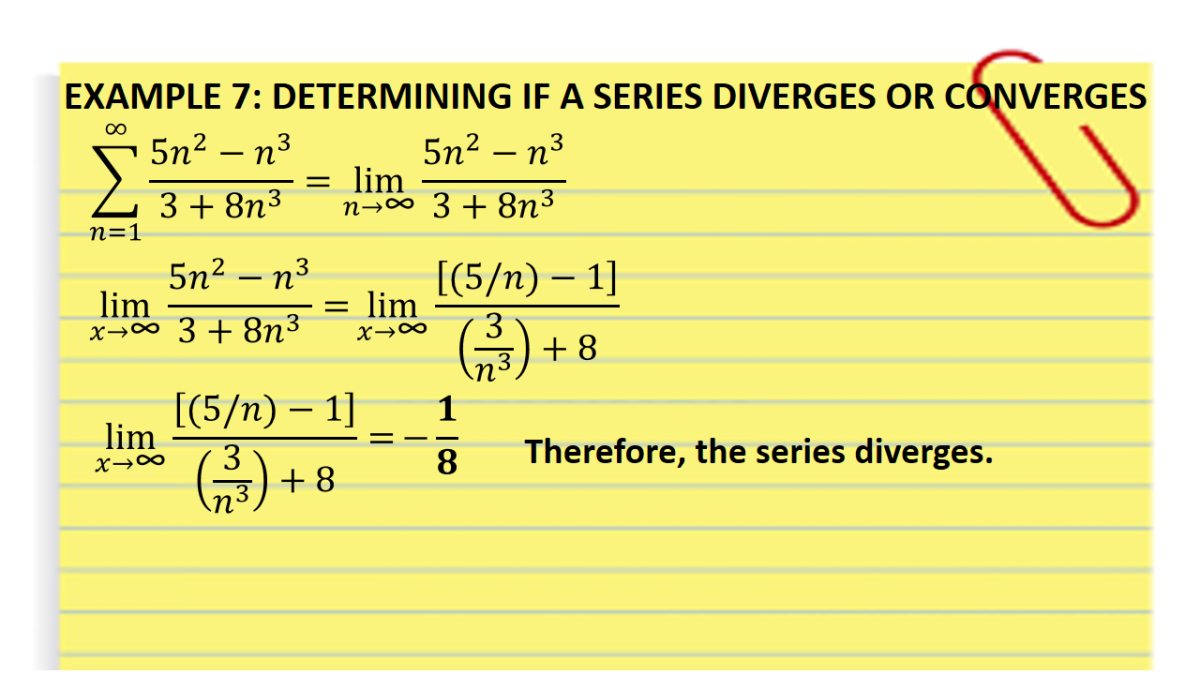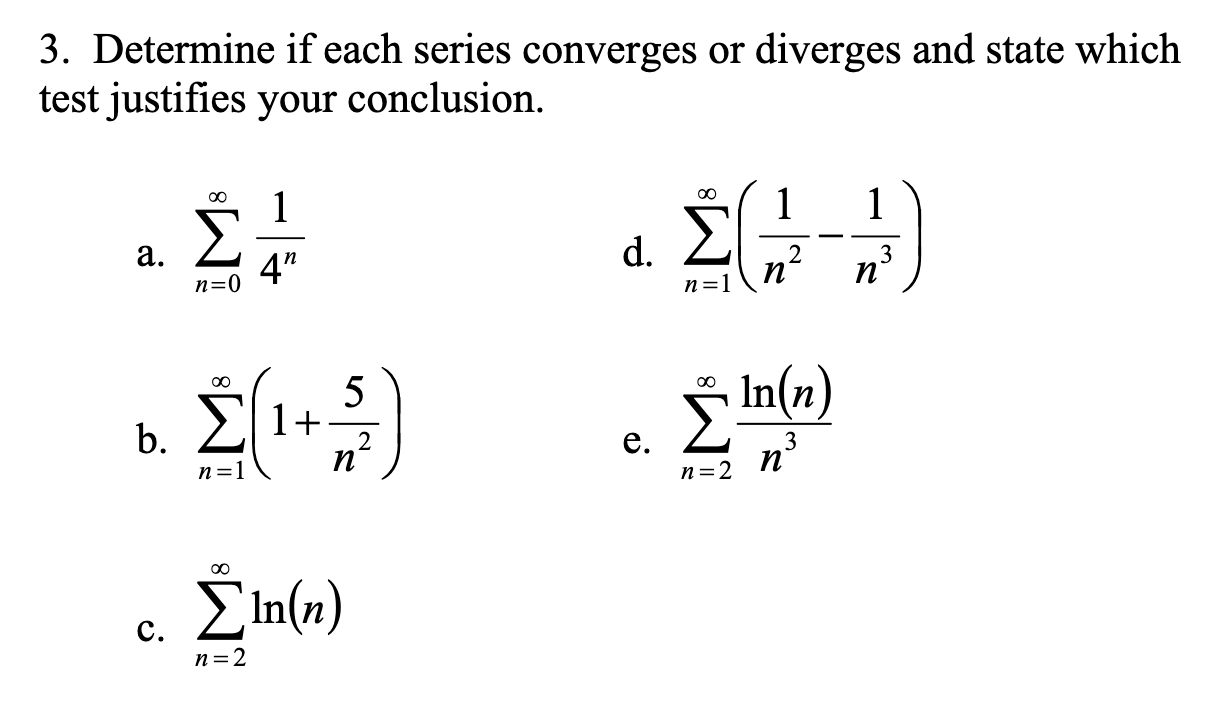Neat Info About How To Tell If A Series Converges

If r < 1, then the series is absolutely convergent. Result how can i graph a series?how can i tell if a series converges or diverges?in this video we guide you through determining the. Longer answer, there exist sequences who converge whose series does not as well as sequences who converge whose series does.

how to keep pandora from timing out how to learn jazz piano how to fix null pointer exception how to lose excess fat fast how to look after an injured bird how to get rid of being sore how to get a free account on world of warcraft how to get a jetpack in poptropica

Ex 2 Determine if an Series and an Alternating Series Converge or

Ex 2 Determine If An Series And Alternating Converge Or

Solved Tell If Each Series Converges Or Diverges, And Which

Divergence Test Determining If A Series Converges Or Diverges Owlcation

Which Geometric Series Converges?

Ex 1 Determine if an Series and an Alternating Series Converge or

Ex 1 Determine If An Series And Alternating Converge Or

Result the geometric series test determines the convergence of a geometric series.

How to tell if a series converges. 970k views 3 years ago new calculus video playlist. Does a sequence have to converge if n approaches infinity if it's series converges or are they mutually exclusive? Its limit exists and is finite) then the series is also called convergent and in this case if lim n→∞sn = s lim n → ∞ s n = s then, ∞ ∑ i=1ai = s ∑ i = 1 ∞ a i = s.

Assume that for all n, is not zero. There is an impressive repository of tools that can. Before we can learn how to determine the convergence or divergence of.

Result how can we tell whether a series converges or diverges? If lim k → ∞ak ≠ 0, then ∞ ∑ k = 0ak diverges. Result if the sequence of partial sums is a convergent sequence ( i.e.

Result if the series ∞ ∑ n = 1 | an | converges then the series ∞ ∑ n = 1an also converges. For example, how do you construct the function on the. The inverse is not true.

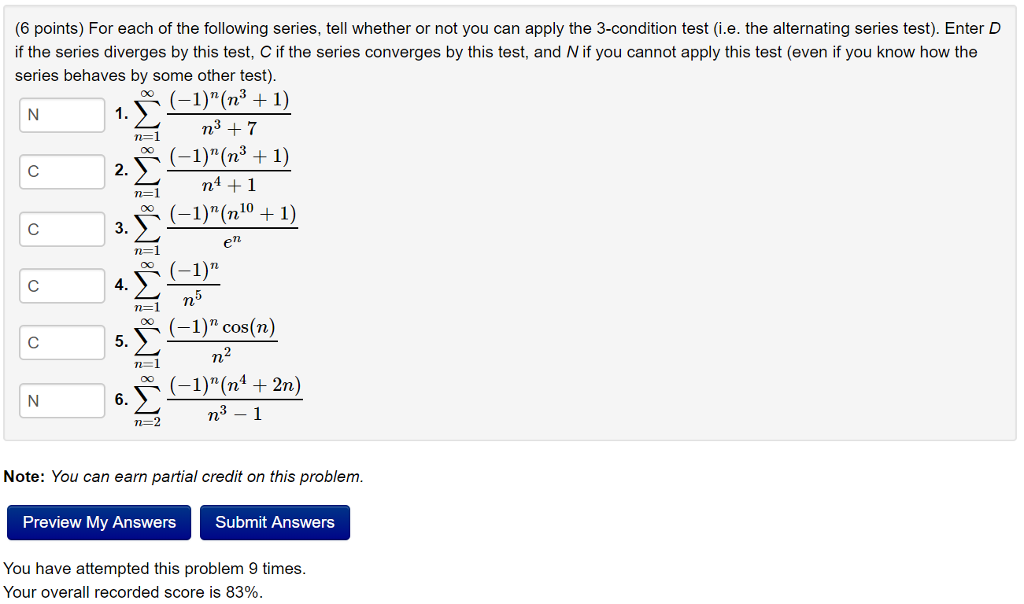
1/n^2 is a good example. Result in this section we explore series whose summation includes negative terms. Result the partial sums form a sequence ${s_k}$.

Result since we’ve shown that the series, $\sum_{n=1}^{\infty} \dfrac{1}{2^n}$, is convergent, and $\dfrac{1}{2^n} > \dfrac{1}{2^n + 4}$, we can. Result given a function series, what are the ways often used to find the function that the series converges to? Suppose that there exists such that.

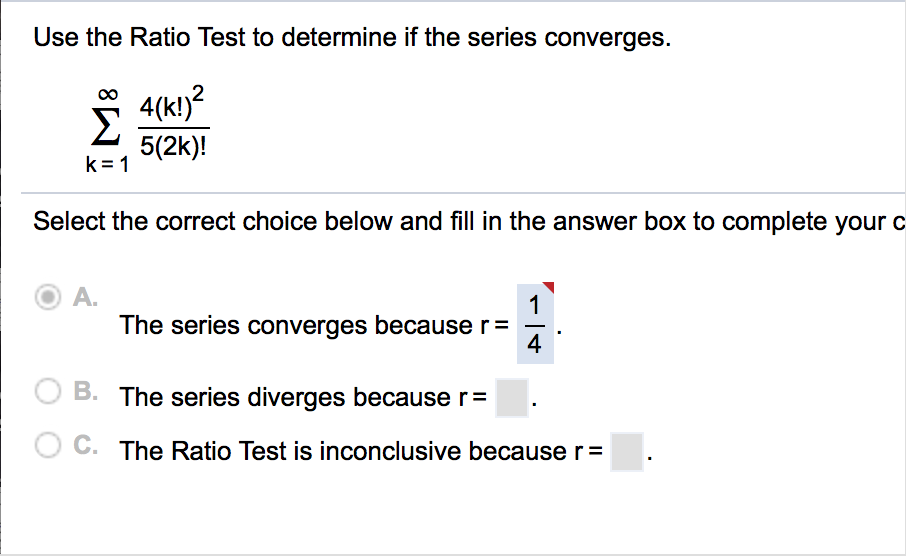
Result all series either converge or do not converge. This test determines whether the series is divergent or not, where. If r > 1, then the series diverges.

This calculus 2 video tutorial provides a basic introduction into series. Result there are many ways to test a sequence to see whether or not it converges. Result is a geometric series and we know that since |r| = |1 3| < 1 the series will converge and its value will be, ∞ ∑ n = 0 1 3n = 1 1 − 1 3 = 3 2.

The series ∞ ∑ k = 0 k 2k + 1 diverges, since lim k → ∞ k 2k + 1 = 1 / 2 ≠ 0. Result mar 10, 2021 at 16:12. Series convergence tests in alphabetical order.

Sometimes all we have to do is evaluate the limit of the sequence at. That is, absolute convergence implies convergence. By definition, a series that does not converge is said to diverge.